문제 링크: 1504번: 특정한 최단 경로
나의 풀이
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
const fs = require("fs");
const inputs = fs.readFileSync("input").toString().split("\r\n");
const [N, M] = inputs[0].split(" ").map((value) => parseInt(value));
const graph = Array.from({ length: N + 1 }, () => []);
const [v1, v2] = inputs[M + 1].split(" ").map((value) => parseInt(value));
for (let i = 1; i <= M; i++) {
const [from, to, cost] = inputs[i].split(" ").map((value) => parseInt(value));
graph[from].push([to, cost]);
graph[to].push([from, cost]);
}
class Heap {
constructor() {
this.heap = [];
}
get size() {
return this.heap.length;
}
}
class MinHeap extends Heap {
input(value) {
this.heap.push(value);
this.bubbleUp();
}
bubbleUp(currentIndex = this.size - 1) {
if (currentIndex < 1) return;
const currentNode = this.heap[currentIndex];
const parentIndex = Math.floor((currentIndex - 1) / 2);
const parentNode = this.heap[parentIndex];
if (parentNode.cost <= currentNode.cost) return;
[this.heap[currentIndex], this.heap[parentIndex]] = [
parentNode,
currentNode,
];
this.bubbleUp(parentIndex);
}
pull() {
const min = this.heap[0];
if (this.size === 1) {
return this.heap.pop();
}
this.heap[0] = this.heap.pop();
this.bubbleDown();
return min;
}
bubbleDown(currentIndex = 0) {
const leftIndex = currentIndex * 2 + 1;
const rightIndex = currentIndex * 2 + 2;
const length = this.size;
let parentIndex = currentIndex;
if (
leftIndex < length &&
this.heap[leftIndex].cost < this.heap[parentIndex].cost
) {
parentIndex = leftIndex;
}
if (
rightIndex < length &&
this.heap[rightIndex].cost < this.heap[parentIndex].cost
) {
parentIndex = rightIndex;
}
if (parentIndex !== currentIndex) {
[this.heap[parentIndex], this.heap[currentIndex]] = [
this.heap[currentIndex],
this.heap[parentIndex],
];
this.bubbleDown(parentIndex);
}
}
}
const djikstra = (start) => {
const distance = Array.from({ length: N + 1 }, () => Infinity);
const priorityQ = new MinHeap();
distance[start] = 0;
priorityQ.input({ node: start, cost: 0 });
while (priorityQ.size > 0) {
const { node: now, cost: nowCost } = priorityQ.pull();
for (const [next, nextCost] of graph[now]) {
if (distance[next] <= nowCost + nextCost) continue;
distance[next] = nowCost + nextCost;
priorityQ.input({ node: next, cost: distance[next] });
}
}
if (start === v1) {
return [distance[1], distance[v2], distance[N]];
}
return [distance[1], distance[v1], distance[N]];
};
const [start_v1, v1_v2, v1_end] = djikstra(v1);
const [start_v2, v2_v1, v2_end] = djikstra(v2);
const sumV1 = start_v1 + v1_v2 + v2_end;
const sumV2 = start_v2 + v2_v1 + v1_end;
const answer = sumV1 > sumV2 ? sumV2 : sumV1;
if (answer === Infinity) {
console.log(-1);
} else {
console.log(answer);
}
이 문제는 v1과 v2를 꼭 지나야 되며, 양방향 그래프이기 때문에 start에서 v1까지의 최솟값과 v1에서 start까지 최솟값이 같음을 활용해서 풀었다.
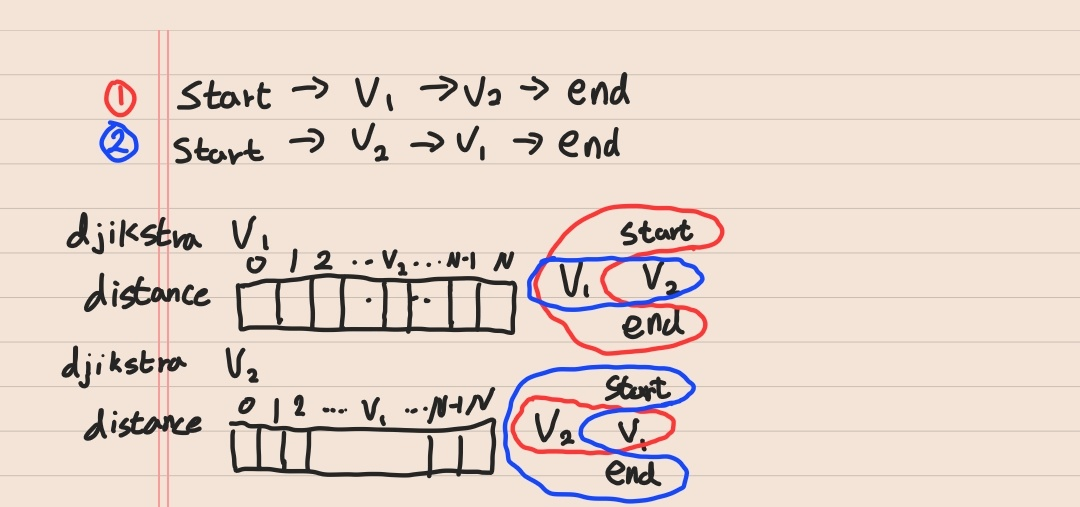
- v1과 v2를 다익스트라 알고리즘을 사용해서 각각 1, vT(T는 v1이면 2, v2면 1), N번까지의 최솟값을 구한다.
- 그림과 같이 빨간색과 파란색 각각의 값을 구한다.
- 가장 작은 값을 answer에 저장 후 answer가 Infinity라면 -1을 출력하고, 그렇지 않다면 answer 값을 출력한다.
Feedback
처음 문제를 접했을 땐 노드 하나씩 탐색하고 dfs의 메모이제이션을 활용해서 풀 생각이었다. 하지만 계산을 해보니 오래 걸리고 다익스트라 문제가 아닌 거 같아서 이 방법은 포기하게 되었다. 다시 문제를 읽으면서 생각을 해보니 시작 지점과 끝 지점은 고정되어 있고 v1과 v2가 다르다는 것을 알게 되었다. 또한 양방향 그래프라는 점과 같이 생각을 해보니 다익스트라 시작 지점을 v1과 v2로 두 번만 사용하는 것이 어떤가를 생각하게 되었다. 다음 문제풀이는 의외로 간단하게 되어 생각을 조금 깊게 하면 풀 수 있는 문제였던 거 같다.